Flow and Solute Transport in Unsaturated Porous Media with Variable Water Content
Researchers:
Dongxiao Zhang, Los Alamos National Laboratory
Thomas Harter, University of California, Davis
Mathematical models of flow and contaminant transport in highly heterogeneous (variable) sediments, while mathematically complicated, are greatly simplifying nature's complexities. Yet they are extremely powerful:
- They provide scientists with fundamental insight into the behavior of water flow and contaminant transport through aquifers with highly variable geologic-sedimentologic architecture. It turns out that if we consider water flow or contaminant transport over distances of several tens of feet (field scale) or several thousands of feet (regional scale), its behavior is fundamentally different from what we observe at the laboratory scale, where measurements are made on small samples (an inch or few inches in length). With mathematical models that account for the sedimentologic heterogeneity, many of these discrepancies can be explained.
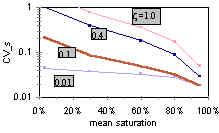
- These mathematical models provide a tool to predict the certainty or uncertainty of predictions in future groundwater flows and future groundwater contamination. Because we can never know the exact geologic properties of an aquifer at each and all locations, predictions of groundwater flow and contaminant transport are necessarily associated with uncertainty. By mathematically or statistically describing the character or type of heterogeneity in aquifers or soils, we can say something about the degree of certainty with which we can make predictions.
This particular project specifically investigates water flow and contaminant transport from the land surface to the water table, where pores are only partly filled with water. (Hence the name 'unsaturated' flow and transport). Depending on whether sediments are tight or fairly coarse, water content in these pores can change quickly. Unlike previous models, the mathematical model that we developed takes into account that water content can be highly variable. In our research paper, we describe the mathematical model and demonstrate how important it is to include a measure for variable water content, particularly when evaluating water flow and contaminant transport in relatively dry soils (where flow and transport happens only over long periods of time, that is, months or years).
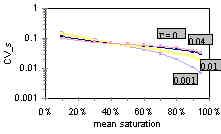
References:
Harter, T., and D. Zhang, Water flow and solute spreading in heterogeneous soils with spatially variable water content, Water Resour. Res., 35(2), 415-426, 1999.
Harter, T., T.C.J. Yeh, Flow in unsaturated random porous media, nonlinear numerical analysis, and comparison to analytic stochastic models, Adv. in Water Resour., 22(3), 257-272, 1998.
Harter, T., T.C.J. Yeh, 1996, Stochastic analysis of solute transport in heterogeneous, variably saturated
porous media, Water Resour. Res.,20, 1585-1595
Harter, T., T.C.J. Yeh, 1996, Conditional stochastic analysis of solute transport in heterogeneous,
variably saturated soils, Water Resour. Res., 20, 1597 - 1609.
Also see:

