Tutorial: Coastal aquifer simulation
content
Coastal aquifer simulation
Coastal aquifer simulation
In this example we will show how to use the mSim toolbox for the simulation of coastal aquifers based on the sharp interface approximation [Mantoglou el al., 2004].
Contents
Mesh generation
mSim solves the partial differencial equation of groundwater flow using finite element method (FEM). The first step of FEM is the mesh generation. However prior to this we need to desribe the geometry of the simulated domain as a combination of primitive objects such as points, lines, etc.
In this exercise we obtain the geometry from shapefiles.
First we read the domain outline:
data_path = '/media/giorgos/Win7/WorkSpace/Santorini_mSim/GIS_DATA_modified/'; domain = shaperead([data_path 'simplify_outline_p']);
and secondly the wells
wells = shaperead([data_path 'wells']);
To generate the mesh we first initialize an empty Constructive Solid Geometry (CSG) object:
santorini = CSGobj_v2(2,1,500,1000,10); % Dim,Npoly,Nline,Npoints,usertol
Next we put the domain outline into the empty object
santorini = santorini.readshapefile(domain);
We can plot anytime the content of the CSG object using the method:
santorini.plotCSGobj axis equal; axis off
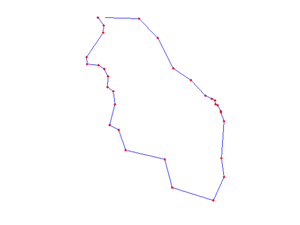
Next we put the wells into the object. However we need to clean up first because not all the points of the shapefile are inside the domain. In addition we want to add few more fields which instruct how Gmsh should refine the mesh around the wells. Here we specify the minimum element length near the wells equal to 10 m and the maximum element length equal to 500 m at 1 km distance from the wells.
dlt = []; for i = 1:size(wells) in = inpolygon(wells(i,1).X, wells(i,1).Y, domain.X, domain.Y); if in wells(i,1) = wells(i,1); wells(i,1).DistMin = 5; wells(i,1).DistMax = 1000; wells(i,1).LcMin = 5; wells(i,1).LcMax = 500; else dlt = [dlt; i]; end end wells(dlt,:)=[];
Finaly we add the wells into the CSG and plot the result
santorini = santorini.readshapefile(wells); santorini.plotCSGobj axis equal; axis off
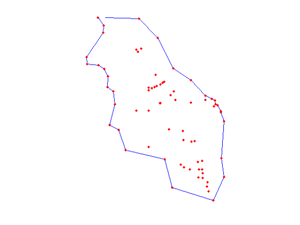
Before generating the mesh we need to define few more options
meshopt=msim_mesh_options; meshopt.lc_gen = 300; meshopt.embed_points = 1;
To generate the mesh we write the geometry and options to a file
santorini.writegeo('santorini',meshopt);
Last we generate the mesh using Gmsh program calling it from Matlab and read it into our workspace
gmsh_path = '/home/giorgos/PROGS/gmsh-2.8.3-Linux/bin/gmsh'; santorini.runGmsh('santorini', gmsh_path, []); [p MSH]=read_2D_Gmsh('santorini',1 ,1);
Info : Running '/home/giorgos/PROGS/gmsh-2.8.3-Linux/bin/gmsh santorini.geo -2' [Gmsh 2.8.3, 1 node, max. 1 thread] Info : Started on Thu Oct 31 20:37:20 2013 Info : Reading 'santorini.geo'... Info : Done reading 'santorini.geo' Info : Meshing 1D... Info : Meshing curve 1 (Line) Info : 41 points found in points clouds (0 edges) Info : Meshing curve 2 (Line) Info : Meshing curve 3 (Line) Info : Meshing curve 4 (Line) Info : Meshing curve 5 (Line) Info : Meshing curve 6 (Line) Info : Meshing curve 7 (Line) Info : Meshing curve 8 (Line) Info : Meshing curve 9 (Line) Info : Meshing curve 10 (Line) Info : Meshing curve 11 (Line) Info : Meshing curve 12 (Line) Info : Meshing curve 13 (Line) Info : Meshing curve 14 (Line) Info : Meshing curve 15 (Line) Info : Meshing curve 16 (Line) Info : Meshing curve 17 (Line) Info : Meshing curve 18 (Line) Info : Meshing curve 19 (Line) Info : Meshing curve 20 (Line) Info : Meshing curve 21 (Line) Info : Meshing curve 22 (Line) Info : Meshing curve 23 (Line) Info : Meshing curve 24 (Line) Info : Meshing curve 25 (Line) Info : Meshing curve 26 (Line) Info : Meshing curve 27 (Line) Info : Meshing curve 28 (Line) Info : Meshing curve 29 (Line) Info : Meshing curve 30 (Line) Info : Meshing curve 31 (Line) Info : Done meshing 1D (0.027553 s) Info : Meshing 2D... Info : Meshing surface 1 (Plane, Delaunay) Info : Done meshing 2D (0.0588942 s) Info : 4670 vertices 9410 elements Info : Writing 'santorini.msh'... Info : Done writing 'santorini.msh' Info : Stopped on Thu Oct 31 20:37:20 2013 13 The file name is santorini.msh Reading nodes... Np = 4670 Reading Elements... Nel = 9410
Because the mesh is 2D triangular we can easily visualize it within matlab
clf triplot(MSH(3,1).elem(1,1).id, p(:,1), p(:,2)) axis equal; axis off
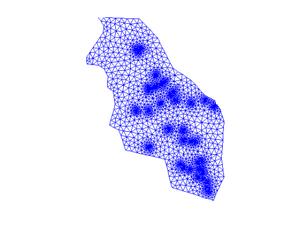
Hydraulic conductivity
The hydraulic condictivity is defined from the following shapefile
cond = shaperead([data_path 'condshp']);
We allocate a variable to hold the hydraulic conductivity on the mesh vertices
K = nan(size(p,1),1);
Then we loop through the hydraulic conductivity polygons and identify the points that lay inside.
for i = 1:size(cond,1) in = inpolygon(p(:,1),p(:,2), cond(i,1).X,cond(i,1).Y); K(in,1) = cond(i,1).KX; end
Due to simplification of the boundaris some points are slightly outside the simplified domain. Therefore we use nearest neibrhood interpolation to assign hydraulic conductivities for those points.
id_nan = find(isnan(K)); id_no_nan = find(~isnan(K)); IDX = knnsearch(p(id_no_nan,:), p(id_nan,:)); K(id_nan,1) = K(id_no_nan(IDX),1);
Groundwater recharge
Similarly to hydraulic conductivity, groundwater recharge is defined from shapefiles
rch = shaperead([data_path 'rchshp']);
Here we will assign the recharge to elements. First we allocate a matrix to hold recharge values
R = zeros(size(MSH(3, 1).elem.id, 1),1);
Next we compute the barycenters of the mesh triangles
cc = Calc_Barycenters(p(:,1:2), MSH(3, 1).elem.id);
Last we loop through the recharge polygons and assign recharge rates to elements
for i = 1:size(rch,1) in = inpolygon(cc(:,1), cc(:,2), rch(i,1).X, rch(i,1).Y); R(in,1) = rch(i,1).RECHARGE; end
In this case the elements outside the rch shapefile get zero recharge. (Note that the recharge shapefile covers only the non zero recharge areas)
To assign the diffuse groundwater recharge we define a structure
FLUX(1,1).id = [1:size(MSH(3, 1).elem.id, 1)]'; % element ids FLUX(1,1).val = R; %element values FLUX(1,1).dim=2; % dimension of the elements FLUX(1,1).el_type='triangle'; % This is the type of element FLUX(1,1).el_order='linear'; % This is the element order FLUX(1,1).id_el=1; % This is the index of the elements in the MSH.elem array
well rates
The actual well rates will be computed from the optimization. Here we will set a constant rate equal to -10 m^3/day. To do so we have to find the node ids that correspond to wells.
FLUXwells = zeros(size(p,1),1); for i = 1:size(wells,1) [dst id] = min(sqrt((wells(i,1).X - p(:,1)).^2 + (wells(i,1).Y - p(:,2)).^2)); FLUXwells(id,1) = -10; end
Boundary conditions
The east and west boundaries are constant head equal to 0 (sea boundary). The north and south are considered impervious boundaries. The east constant head boundary is described be the domain line segments with id 1:15, while the west boundary is described by the line segments with ids 18:31
id_cnst = false(size(p,1),1); for i = 1:14 L = [domain.X(i) domain.Y(i) domain.X(i + 1) domain.Y(i + 1)]; dst = Dist_Point_LineSegment(p(:,1), p(:,2),L); id_cnst(abs(dst - 0)< 0.5) = true; end for i = 18:30 L = [domain.X(i) domain.Y(i) domain.X(i + 1) domain.Y(i + 1)]; dst = Dist_Point_LineSegment(p(:,1), p(:,2),L); id_cnst(abs(dst - 0)< 0.5) = true; end CH = [find(id_cnst) zeros(sum(id_cnst),1)];
to verify that we have identified the correct nodes as boundary conditions its good practice to plot them
plot(p(:,1),p(:,2),'.') hold on plot(p(CH(:,1),1),p(CH(:,1),2),'or') axis equal; axis off
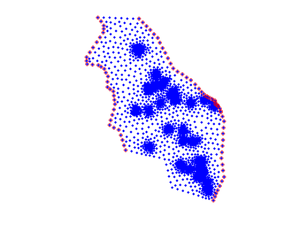
Assemble LHS and RHS matrices
Now we are ready to assemble the system matrices. For the LHS we set the following options and then run:
simopt.dim=2; simopt.el_type='triangle'; simopt.el_order='linear'; [Kglo H]= Assemble_LHS(p, MSH(3,1).elem(1,1).id, K , CH, [], simopt);
Although this is not nessecary we can visualize the sparsity pattern of the conductance matrix.
spy(Kglo)
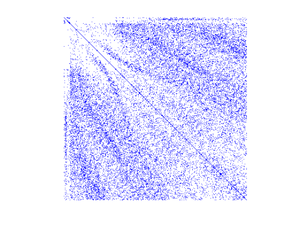
It appears that the mesh numbering by gmsh does not produce very good clustering around the main diagonal. In matlab we can try to improve this by using the available renumbering algorithm such as
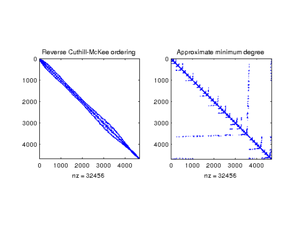
clf renum1 = symrcm(Kglo); subplot(1,2,1);spy(Kglo(renum1,renum1)); title('Reverse Cuthill-McKee ordering') renum2 = symamd(Kglo); subplot(1,2,2);spy(Kglo(renum2,renum2)); title('Approximate minimum degree') % Last we assemble the RHS F_rch= Assemble_RHS(length(H),p, MSH, FLUX); F = F_rch + FLUXwells;
Solve
To solve the system we simply execute:
PHI=solve_system(Kglo(renum1,renum1), H(renum1), F(renum1));
Note that during the solution we use the renumbering from the Reverse Cuthill-McKee ordering algorithm, yet the renumbering affects the matrices during the execution of the "solve_system" command and the matrices do not actually change.
The solution PHI corresponds to the new numbering set by renum1. To revert back to the original numbering we have to find the current row of each vertex. This is quite simple task as follows:
[lia locb] = ismember([1:size(p,1)],renum1); PHI = PHI(locb);
However this is not the hydraulic head field, but the potential Φ . To convert it to hydraulic head we use the following formula from [Mantoglou el al., 2004]
Head = sign(PHI).*sqrt(2*0.025.*abs(PHI)/(1+0.025));
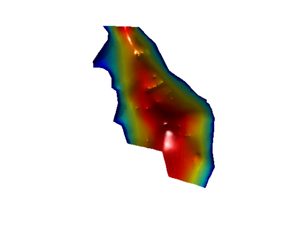
Since we are using 2D triangle elements we can visualize the solution
clf trisurf(MSH(3,1).elem(1,1).id, p(:,1), p(:,2),Head,'edgecolor','none',... 'FaceColor','interp','FaceLighting','phong') camlight right view(0,90);axis off;daspect([2500 2500 1])
<!--
